Mots-Clés : Mécanique du contact (M. Barboteu, M. Sofonea) ; Élasticité et Plasticité (M. Sofonea) ; EDP pour la Mécanique (M. Barboteu, M. Sofonea) ; Méthodes géométriques (R. Brouzet) et variationnelles (M. Sofonea) ; Approximation et simulation numériques (M. Barboteu, F. Bonaldi, M. David, D. Defour, S. Dumont) ; Algorithmes numériques pour le Calcul Haute Performance (D. Defour)
La thématique Modélisation Mathématique et Numérique pour la Mécanique recouvre plusieurs objectifs :
- la description de modèles physiques par des équations aux dérivées partielles (principalement issues de la Mécanique des Milieux Continus),
- l’analyse mathématique avec des méthodes géométriques et variationnelles,
- l’analyse numérique de ces modèles et la simulation numérique.
Ce thème de recherche consiste à étudier des Equations aux Dérivées Partielles (EDP) issues de la Mécanique des Milieux Continus (élasticité, hyperélasticité, viscoplasticité, mécanique des fluides), et notamment les équations d’évolution modélisant les problèmes de contact avec ou sans frottement. Les phénomènes de contact impliquant des corps déformables abondent dans l’industrie et dans la vie de tous les jours ; ils sont variés, fortement non linéaires et complexes; ils jouent un rôle important dans les structures et les systèmes mécaniques, et leur étude complète implique des compétences variées, allant de la mécanique au calcul scientifique, en passant par l’analyse fonctionnelle et l’analyse numérique. Souvent, il s’agit également de problèmes faisant intervenir des couplages avec des phénomènes autres que la mécanique (thermique, magnétique, acoustique, hydraulique etc.) ; de plus, le domaine de calcul présente, parfois, des complexités géométriques notables, d’où la nécessité de méthodes numériques compatibles avec l’utilisation de maillages généraux.
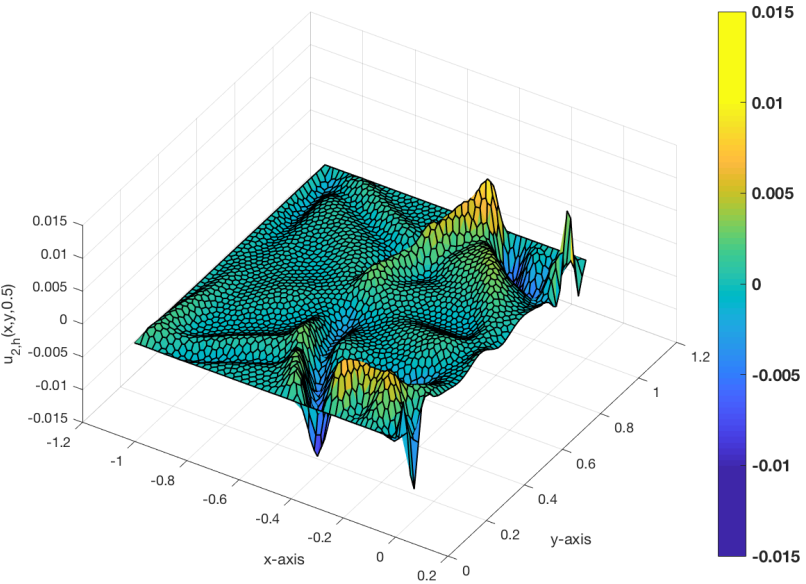
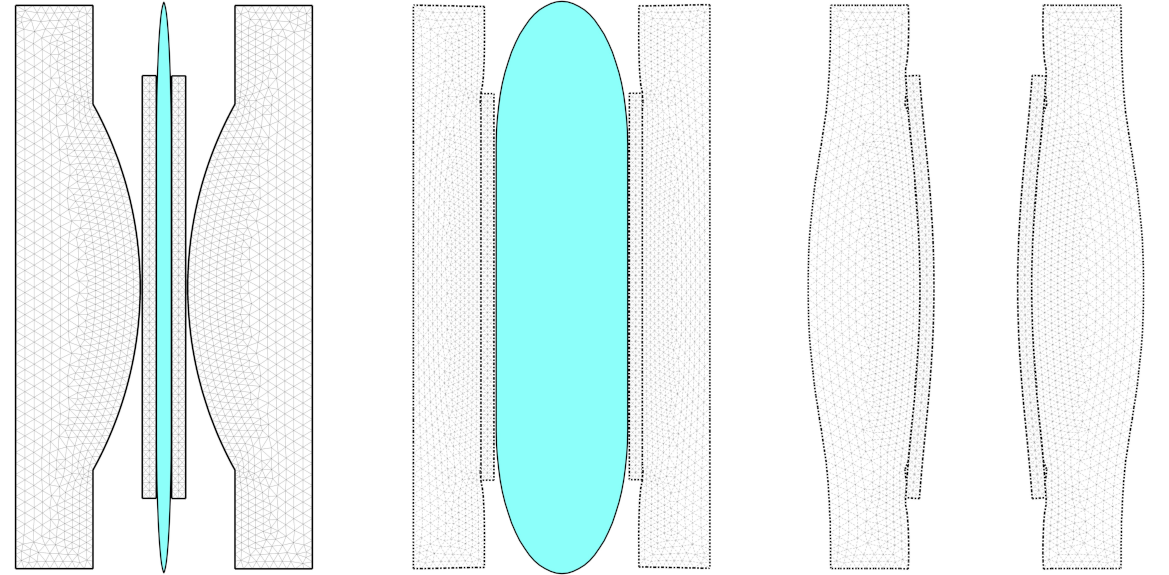
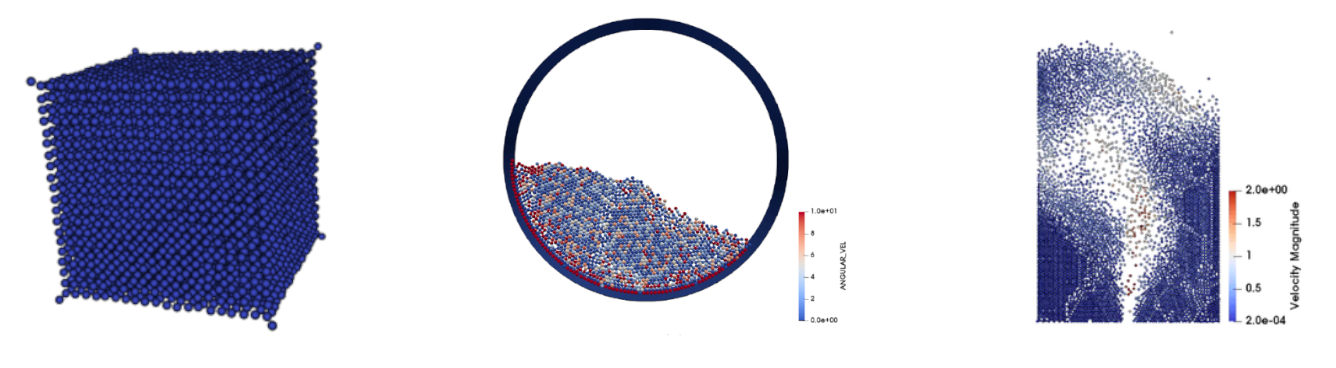
Notre objectif est de présenter une description claire et précise des problèmes d’EDP provenant de la Mécanique ainsi que de réaliser leur analyse mathématique en utilisant des méthodes géométriques, variationnelles et numériques. Ainsi, nous avons considéré des modèles mécaniques originaux comme par exemple les phénomènes sous-jacents au contact (frottement, usure, adhésion, effets thermiques dans les milieux déformables et granulaires). Nous avons alors proposé des formulations variationnelles associées à ces modèles non réguliers, non linéaires et parfois non-convexes, puis nous avons démontré des résultats allant de l’existence et l’unicité des solutions faibles, à l’étude de l’erreur d’approximation pour les schémas discrétisés. Par ailleurs, afin de vérifier les différentes études théoriques et de résoudre ces problèmes, nous avons mis en œuvre de nombreux modèles numériques, souvent associés à des systèmes non réguliers, non convexes, non linéaires et non symétriques de grande taille. Pour cela nous avons développé des méthodes de résolution adaptées à la modélisation mécanique considérée (dynamique, lois non convexes, grandes déformations, contact frottant, viscoplasticité), mais également adaptées aux nouvelles générations d’ordinateurs à architecture parallèle (HPC).
Mise à jour le 9 octobre 2024









