Keywords: Contact Mechanics (M. Barboteu, M. Sofonea); Elasticity and Plasticity (M. Sofonea); PDE for Mechanics (M. Barboteu, M. Sofonea); Geometric (R. Brouzet) and Vaiational Methods (M. Sofonea); Numerical Approximation and Simulation (M. Barboteu, F. Bonaldi, M. David, D. Defour, S. Dumont); Numerical Algorithms for High Performance Computing (D. Defour)
The Mathematical and Numerical Modelling for Mechanics theme covers several objectives :
- Description of physical models using partial differential;
- Mathematical analysis using geometric and variational methods;
- Numerical analysis of these models and numerical situation.
This research theme involves the study of Partial Differential Equations (PDEs) derived from Continuum Mechanics (elasticity, hyperelasticity, viscoplasticity, fluid mechanics), and in particular the evolution equations modeling contact problems with or without friction. Contact phenomena involving deformable bodies abound in industry and everyday life, they are varied, highly non-linear and complex; they play an important role in mechanical structures and systems and their comprehensive study involves a wide range of skills, from mechanics to scientific computing, functional analysis and numerical analysis. Often, these problems also involve coupling with phenomena other than mechanics (thermal, magnetic, acoustic, hydraulic, etc.); moreover, the computational domain sometimes presents notable geometric complexities, hence the need for numerical methods compatible with the use of general meshes.
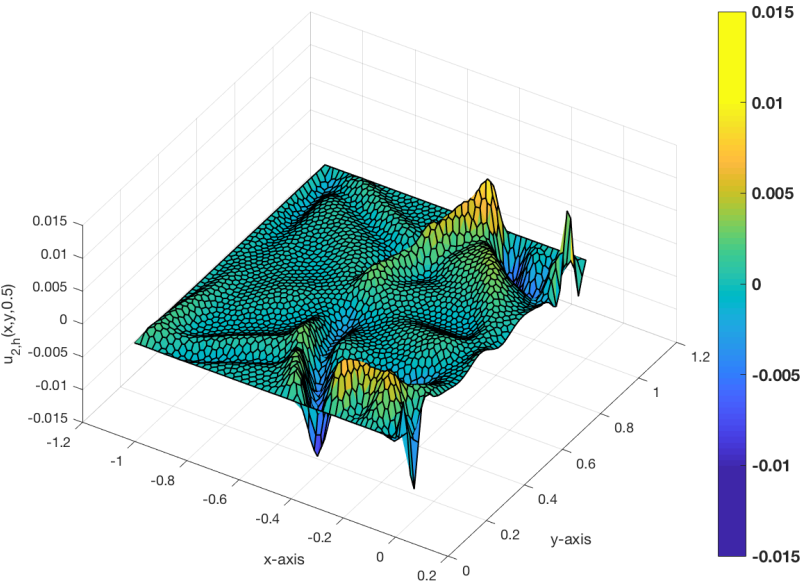
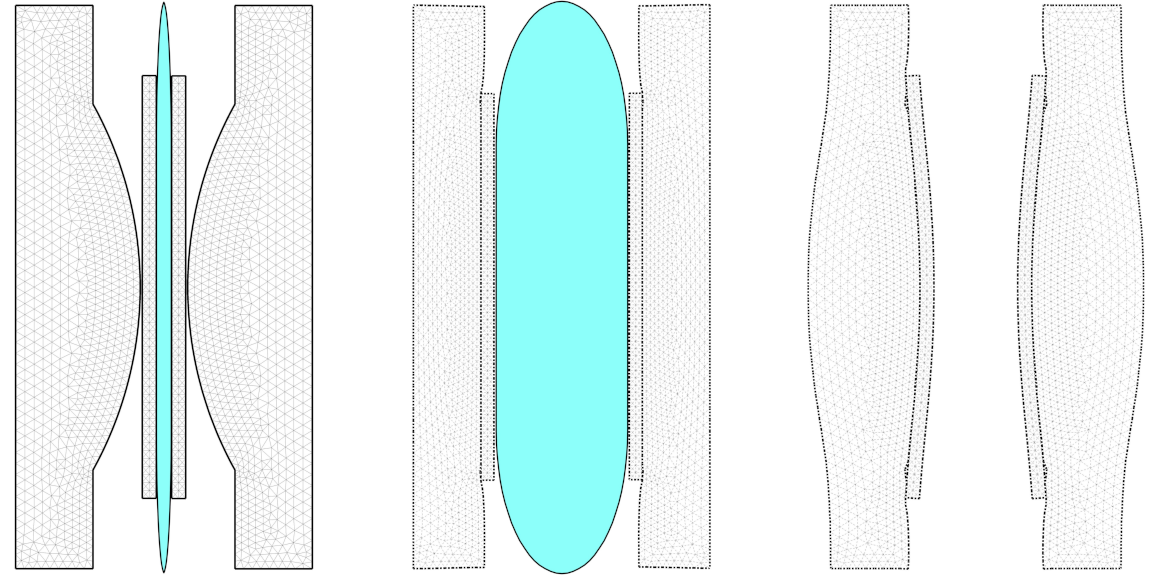
Our aim is to present a clear and precise description of PDE problems orignating in Mechanics, and to carry out their mathematical analysis using geometric, variational and numerical methods. We have considered original mechanical models, such as the phenomena underlying contact (friction, wear, adhesion, thermal effects, in deformable and granula media). We then proposed variational formulations associated with these non-regular, non-linear and sometimes non-convex models, and demonstrated results rangin from the existence and uniqueness of weak solutions, to the study of the approximation error for discretized schemes. Furthermore, in order to verify the various theoretical studies and solve these problems, we have implemented numerous numerical models, often associated with non-regular, non-convex, non-linear and non symmetric systems of large size. To this end, we have developed resolution methods adapted to the mechanical modeling considered (dynamics, non-convex laws, large deformations, frictional contact, viscoplasticity), but also adapted to the new generations of parallel architecture computers (HPC).
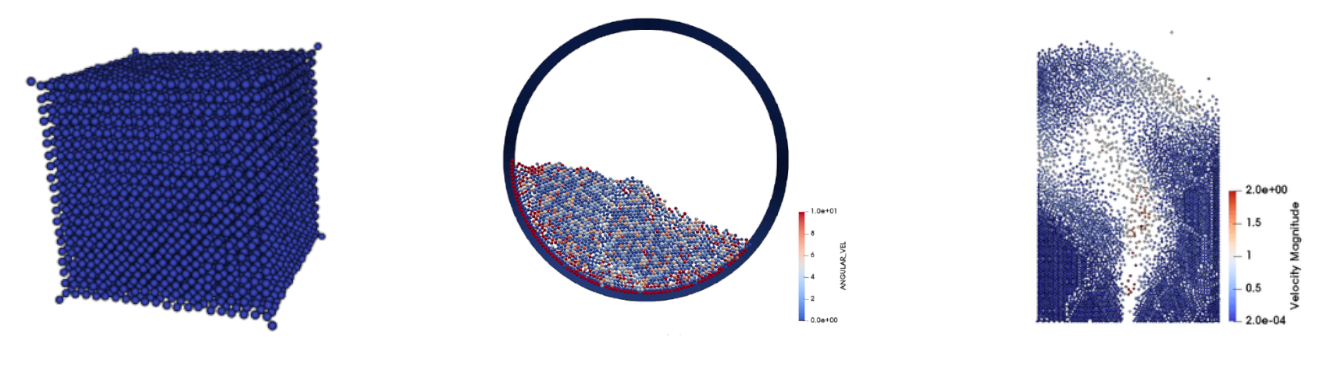
Mise à jour le 3 juillet 2025

